A user defined random variate using the inverse method on a given CDF. More...

#include "libran.h"
#include <math.h>

Include dependency graph for LRuinvcdf.c:

Macros
#define	Abs(a) (((a)<0)?-(a):(a))

#define	Signabs(a, b) ((b)<0?-(a):(a))

#define	Sign(a, b) ((b)<0?-Abs(a):Abs(a))

Functions
int	LRd_uinvcdf (LR_obj o, double(cdf)(double))
	LRd_uinvcdf() - set the user defined CDF for this variate distribution. More...

double	LRd_zeroin (double ax, double bx, double U, double(*f)(double), double tol)
	LRd_zeroin() Routine numerically finds solution to f(x)-U = 0 specialized to CDF()s. More...

double	LRd_uinvcdf_RAN (LR_obj *o)
	LRd_uinvcdf_RAN(LR_obj *o) - double random variate via inverse method of the UserCDF() fn. More...

double	LRd_uinvcdf_PDF (LR_obj *o, double x)
	LRd_uinvcdf_PDF(LR_obj *o, double x) - double probability distribution function approximated from the user supplied cumulative distribution function. More...

double	LRd_uinvcdf_CDF (LR_obj *o, double x)
	LRd_uinvcdf_CDF(LR_obj *o, double x) - double User supplied cumulative distribution function. More...

int	LRf_uinvcdf (LR_obj o, float(cdf)(float))
	LRf_uinvcdf() - set the user defined CDF for this variate distribution. More...

float	LRf_zeroin (float ax, float bx, float U, float(*f)(float), float tol)
	LRf_zeroin() Routine numerically finds solution to f(x)-U = 0 specialized to CDF()s. More...

float	LRf_uinvcdf_RAN (LR_obj *o)
	LRf_uinvcdf_RAN(LR_obj *o) - float random variate via inverse method of the UserCDF() fn. More...

float	LRf_uinvcdf_PDF (LR_obj *o, float x)
	LRf_uinvcdf_PDF(LR_obj *o, float x) - float probability distribution function approximated from the user supplied cumulative distribution function. More...

float	LRf_uinvcdf_CDF (LR_obj *o, float x)
	LRf_uinvcdf_CDF(LR_obj *o, float x) - float User supplied cumulative distribution function. More...

Detailed Description

A user defined random variate using the inverse method on a given CDF.

The user may supply a compliant CDF and these methods will return a random variate by the inverse method and an approximate PDF using the calculus definition of a derivative.

The user supplied CDF must have the following properties where 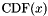$\mbox{CDF}(x)$ is monotonically non-decreasing such that

$\mbox{CDF}(x_1) \le \mbox{CDF}(x_2) \mbox{ where } x_1 < x_2$

and

$0 \le \mbox{CDF}(x) \le 1 \mbox{ for all } x$

.

If any of these requirements are not met and caught the methods will raise the LRerr_InvalidCDF error (amongst other ones).

The supplied CDFs must have the following signature (for double and float respectively:

double UserCDF(double x);
float UserCDF(float x);

where UserCDF is some function name and any attributes are tracked internally or externally (but not passed through the function argument list).

In addition when the user must supply some of the following: Zero, one, or two LR_obj end point attributes (a and b). The LR_obj middle and width (m and s) if either a or are not given.

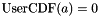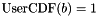These attributes are for the Zeroin method to start with some reasonable guesses of where to bracket the solution. If your CDF has a well defined interval such that $\mbox{UserCDF}(a) = 0$ and $\mbox{UserCDF}(b) = 1$ then setting these attributes are likely the best approach. However, if the CDF is semi-infinite or infinite in range then setting the middle m to either near the mean, median, or mode will be likely sufficient. Note that m does not need to be exact, just a good approximation (e.g. 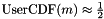$\mbox{UserCDF}(m) \approx \frac{1}{2}$ . The width s should be such that about two thirds of the random variate density lies within about 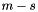$ m - s $ and $ m + s $ . 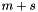In other words, 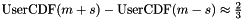$\mbox{UserCDF}(m + s) - \mbox{UserCDF}(m - s) \approx \frac{2}{3}$ . If the function is semi-infinite then give the known endpoint, approximate m and s to handle the semi-infinite part.

#include <math.h>
#include "libran.h"
double MyCDF(double x) {
        static double pi4 = NAN;
        double zero = 0.0, one = 1.0, two = 2.0;
        if (isnan(pi4))
                pi4 = atan(one);
        if (x <= zero) {
                return zero;
        } else if (x >= two) {
                return one;
        } else {
                double t = sin(pi4*x);
                return t*t;
        }
}
int main() {
...
LR_obj *o = LR_new(uinvcdf, LR_double);
...
// set the end points for the zeroin search
LR_set_all(o,"ab", 0., 2.);
// Include the User CDF
if (LRd_uinvcdf(o, MyCDF)) {
        LRperror("Sample Code - uinvcdf", o->errno);
}
...
// do your typical processing
...
// remove the LR_obj
LR_rm(&o);
...
}

The probability and cumulative distribution functions for the above user defined CDF is:

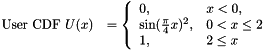
$\begin{eqnarray*} \mbox{User CDF } U(x) &= \left\{ \begin{array}{ll} 0, & x < 0, \\ \sin(\frac{\pi}{4}x)^2, & 0 < x \le 2 \\ 1, & 2 \le x \end{array} \right. \end{eqnarray*}$

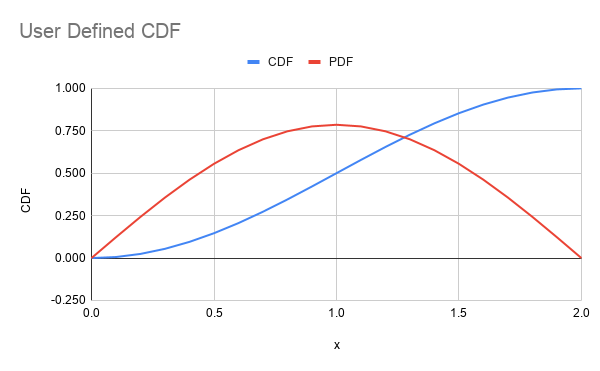
Definition in file LRuinvcdf.c.

Function Documentation

◆ LRd_uinvcdf()

int LRd_uinvcdf	(	LR_obj *	o,
		double(*)(double)	cdf
	)

LRd_uinvcdf() - set the user defined CDF for this variate distribution.

Parameters

o	LR_obj object
cdf	User defined CDF

Returns: 0 if no error, non-zero otherwise

Definition at line 131 of file LRuinvcdf.c.

◆ LRd_uinvcdf_CDF()

double LRd_uinvcdf_CDF	(	LR_obj *	o,
		double	x
	)

LRd_uinvcdf_CDF(LR_obj *o, double x) - double User supplied cumulative distribution function.

Parameters

o	LR_obj object
x	value

Returns: double CDF at x

Definition at line 384 of file LRuinvcdf.c.

◆ LRd_uinvcdf_PDF()

double LRd_uinvcdf_PDF	(	LR_obj *	o,
		double	x
	)

LRd_uinvcdf_PDF(LR_obj *o, double x) - double probability distribution function approximated from the user supplied cumulative distribution function.

Use the definition of a derivative to approximate the PDF from the given CDF.

Parameters

o	LR_obj object
x	value

Returns: double PDF at x

Definition at line 329 of file LRuinvcdf.c.

◆ LRd_uinvcdf_RAN()

double LRd_uinvcdf_RAN ( LR_obj * o )

LRd_uinvcdf_RAN(LR_obj *o) - double random variate via inverse method of the UserCDF() fn.

Parameters

o	LR_obj object

Returns: double

Definition at line 269 of file LRuinvcdf.c.

◆ LRd_zeroin()

double LRd_zeroin	(	double	ax,
		double	bx,
		double	U,
		double(*)(double)	f,
		double	tol
	)

LRd_zeroin() Routine numerically finds solution to f(x)-U = 0 specialized to CDF()s.

LRd_zeroin() finds the zero of (f(x) - U) within the interval [ax,bx]. It is assumed that f(ax) - U and f(bx) - U have opposite signs without checking. LRd_zeroin returns a zero x in the given interval [ax,bx] to within a tolerance 2*eps*abs(x) + tol, where eps is the relative machine precision such that eps is the smallest number + 1 that is different from 1.

This is based on the subroutine ZEROIN() in FMMLIB presented in "Introduction to Numerical Analysis" by Forsythe, Malcolm, and Moler, which is a slightly modified translation of the ALGOL 60 procedure ZERO given by Richard Brent, "Algorithms for Minimization without Derivatives", Prentice-Hall, Inc. (1973).

by R.K.Owen,Ph.D. 1994/04/18

Parameters

ax	left endpoint of the initial interval
bx	right endpoint of the initial interval
U	Uniform random variate of where to find x such that f(x) = U
f	function subprogram which evaluates f(x) for any x in the interval [ax,bx]
tol	desired length of the interval of uncertainty of any final result ( must be >= 0.) (Always set to zero here.)

Returns: double the value x such that UserCDF(x) - U = 0

Definition at line 170 of file LRuinvcdf.c.

◆ LRf_uinvcdf()

int LRf_uinvcdf	(	LR_obj *	o,
		float(*)(float)	cdf
	)

LRf_uinvcdf() - set the user defined CDF for this variate distribution.

Parameters

o	LR_obj object
cdf	User defined CDF

Returns: 0 if no error, non-zero otherwise

Definition at line 413 of file LRuinvcdf.c.

◆ LRf_uinvcdf_CDF()

float LRf_uinvcdf_CDF	(	LR_obj *	o,
		float	x
	)

LRf_uinvcdf_CDF(LR_obj *o, float x) - float User supplied cumulative distribution function.

Parameters

o	LR_obj object
x	value

Returns: float CDF at x

Definition at line 666 of file LRuinvcdf.c.

◆ LRf_uinvcdf_PDF()

float LRf_uinvcdf_PDF	(	LR_obj *	o,
		float	x
	)

LRf_uinvcdf_PDF(LR_obj *o, float x) - float probability distribution function approximated from the user supplied cumulative distribution function.

Use the definition of a derivative to approximate the PDF from the given CDF.

Parameters

o	LR_obj object
x	value

Returns: float PDF at x

Definition at line 611 of file LRuinvcdf.c.

◆ LRf_uinvcdf_RAN()

float LRf_uinvcdf_RAN ( LR_obj * o )

LRf_uinvcdf_RAN(LR_obj *o) - float random variate via inverse method of the UserCDF() fn.

Parameters

o	LR_obj object

Returns: float

Definition at line 551 of file LRuinvcdf.c.

◆ LRf_zeroin()

float LRf_zeroin	(	float	ax,
		float	bx,
		float	U,
		float(*)(float)	f,
		float	tol
	)

LRf_zeroin() Routine numerically finds solution to f(x)-U = 0 specialized to CDF()s.

LRf_zeroin() finds the zero of (f(x) - U) within the interval [ax,bx]. It is assumed that f(ax) - U and f(bx) - U have opposite signs without checking. LRf_zeroin returns a zero x in the given interval [ax,bx] to within a tolerance 2*eps*abs(x) + tol, where eps is the relative machine precision such that eps is the smallest number + 1 that is different from 1.

This is based on the subroutine ZEROIN() in FMMLIB presented in "Introduction to Numerical Analysis" by Forsythe, Malcolm, and Moler, which is a slightly modified translation of the ALGOL 60 procedure ZERO given by Richard Brent, "Algorithms for Minimization without Derivatives", Prentice-Hall, Inc. (1973).

by R.K.Owen,Ph.D. 1994/04/18

Parameters

ax	left endpoint of the initial interval
bx	right endpoint of the initial interval
U	Uniform random variate of where to find x such that f(x) = U
f	function subprogram which evaluates f(x) for any x in the interval [ax,bx]
tol	desired length of the interval of uncertainty of any final result ( must be >= 0.) (Always set to zero here.)

Returns: float the value x such that UserCDF(x) - U = 0

Definition at line 452 of file LRuinvcdf.c.

Macros

Functions

Detailed Description

Function Documentation

◆ LRd_uinvcdf()

◆ LRd_uinvcdf_CDF()

◆ LRd_uinvcdf_PDF()

◆ LRd_uinvcdf_RAN()

◆ LRd_zeroin()

◆ LRf_uinvcdf()

◆ LRf_uinvcdf_CDF()

◆ LRf_uinvcdf_PDF()

◆ LRf_uinvcdf_RAN()

◆ LRf_zeroin()